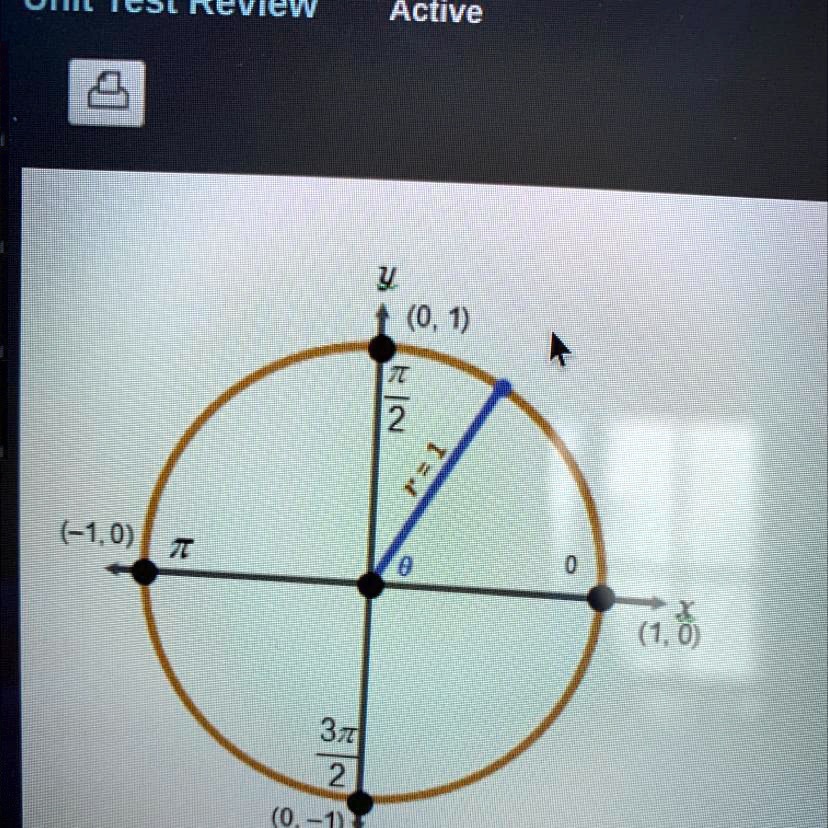
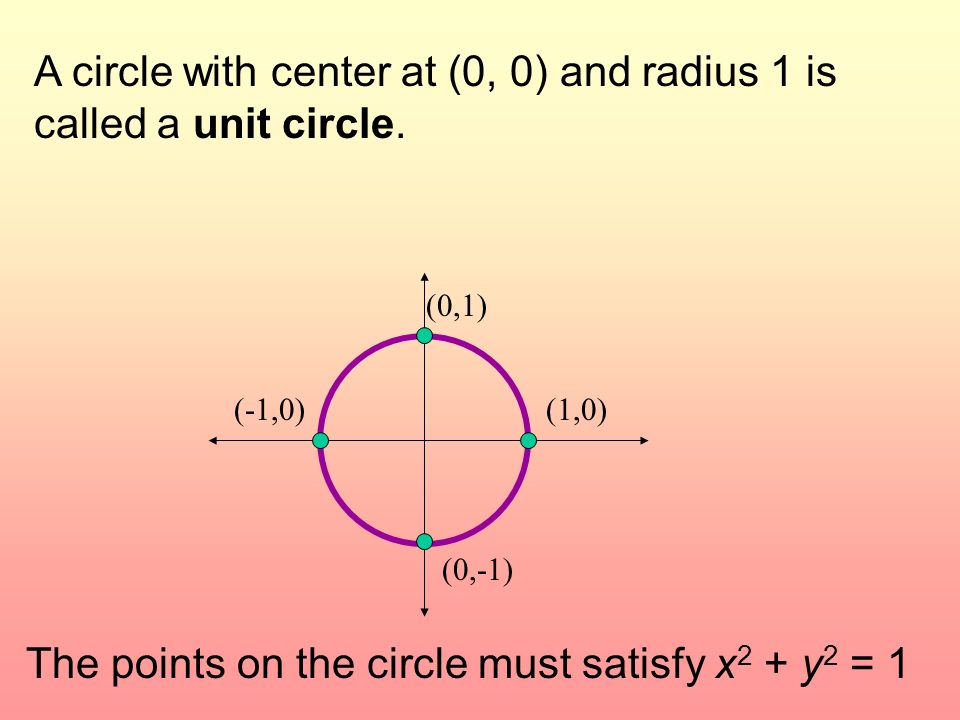
[最も選択された] unit circle x^2 y^2=1 230939-The base is the unit circle x^2+y^2=1

To see if the given angle is related to one of the basic reference angles whose values I've memorized, I'll subtract the given angle from the angle measure at the upper end of QIII, beingQuestion The area (in sq units) of the part of the circle x 2y 2=36, which is outside the parabola y 2=9x is A 24π3 3 B 12π−3 3 C 24π−3 3 D 12π3 3 Medium Solution Verified by Toppr CorrectX 2 y 2 = 1 x^2 y^2 = 1 x 2 y 2 = 1 If we stretch in both the x x x and y y y directions and distribute the powers of two through the parentheses, we get x 2 a 2 y 2 b 2 = 1

5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts

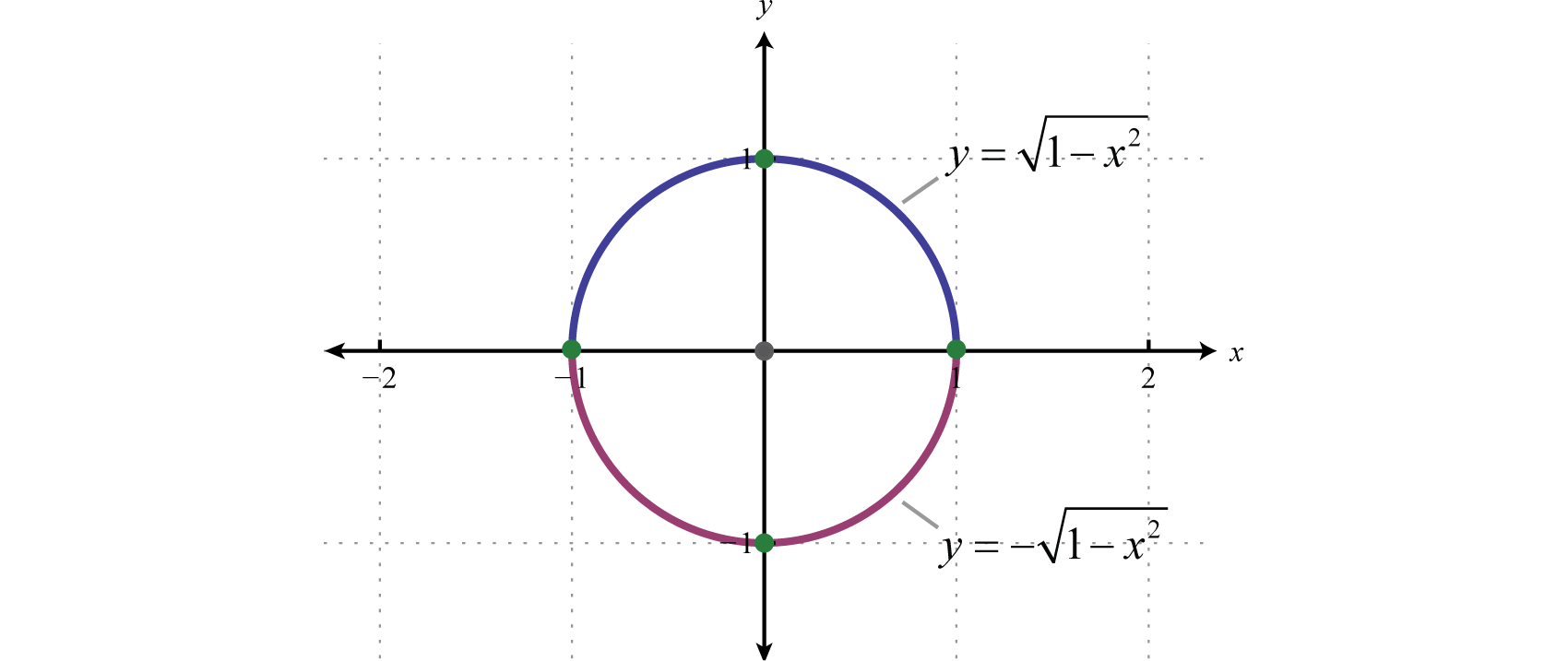
The base is the unit circle x^2+y^2=1

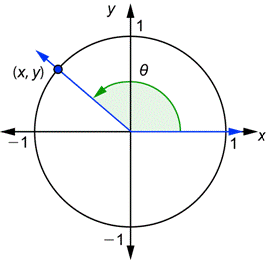
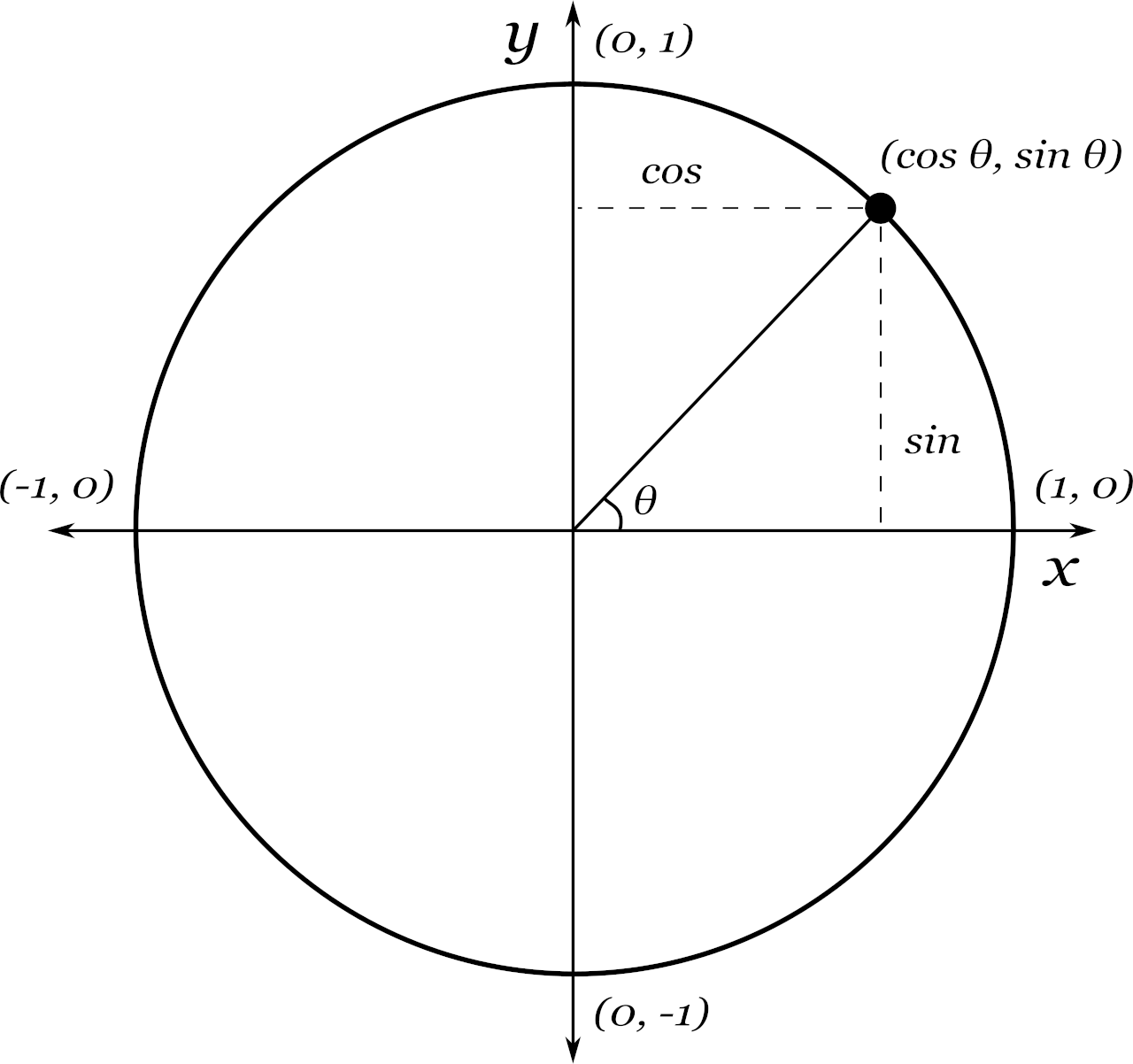
The base is the unit circle x^2+y^2=1-0 votes 1 answer FindThe trigonometric functions cosine and sine of angle θ may be defined on the unit circle as follows If (x, y) is a point on the unit circle, and if the ray from the origin (0, 0) to (x, y) makes an angle θ

Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download

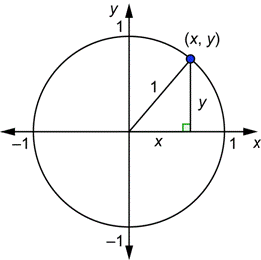
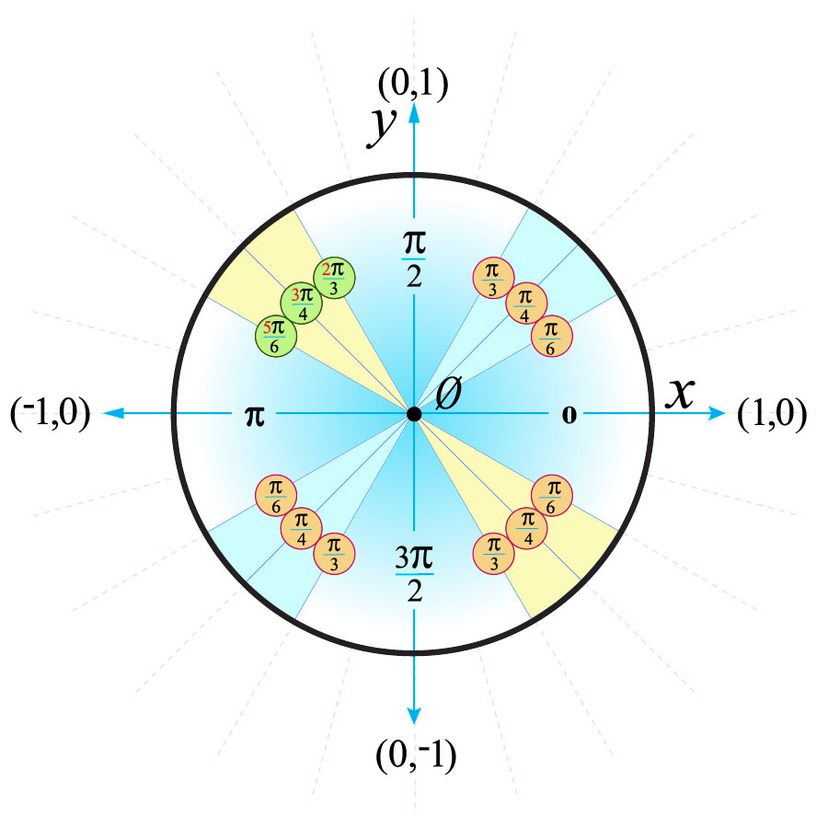
For quadrantral angles, the corresponding point on the unit circle falls on the x or yaxis In that case, we can easily calculate cosine and sine from the values of x x and y y Example 2Based on the Pythagorean Theorem, the equation of the unit circle is therefore x 2 y 2 = 1 This is true for all points on the unit circle, not just those in the first quadrant, and is useful for defining In a unit circle, any line that starts at the center of the circle and ends at its perimeter will have a length of 1 So, the longest side of this triangle will have a length of 1 The longest side

Is divided into three arcs by choosing three random points A,B,C on the circle (independently and uniformly), forming arcs between A and B, between A and C, and between B and CFree Circle calculator Calculate circle area, center, radius and circumference stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree toThis means that we can rewrite the equation of the circle, $x^2 y^2 = r^2$, in terms of $t$ We can do this by assigning a special function for $x$ and $y$ – this is where the unit circle and

 Explanation Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k)At what points will the line y = x intersect the unit circle x2 y2 = 1?From the unit circle with tangent, we can clearly see that tan is NOT defined for the angles π/2 and 3π/2 So we get vertical asymptotes at x = π/2 and at x = 3π/2 in the graph of tangent function

Deformation Of The Unit Circle S X 2 Y 2 1 In The Plane Z 1 Download Scientific Diagram

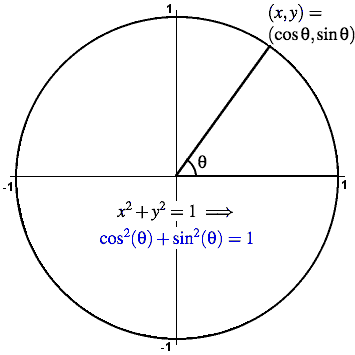
Trigonometry Facts The Amazing Unit Circle

(x, y) = (smaller xvalue) %3D (х, у) (larger xvalue) Question Transcribed Image Text At what points will the line y = xFinally, we note that we can identify any point on the unit circle exactly simply by choosing one of its coordinates Since every point (x,y) ( x, y) on the unit circle satisfies the equation x2y2 = 1, x 2Evaluate the line integral R C (2 x 2 y) ds, where C is the upper half of the unit circle x 2 y 2 = 1 Show transcribed image text Expert Answer Who are the experts?

1

Find The Points On The Unit Circle X 2 Y 2 1 Nearest And Farthest From 1 1 Snapsolve

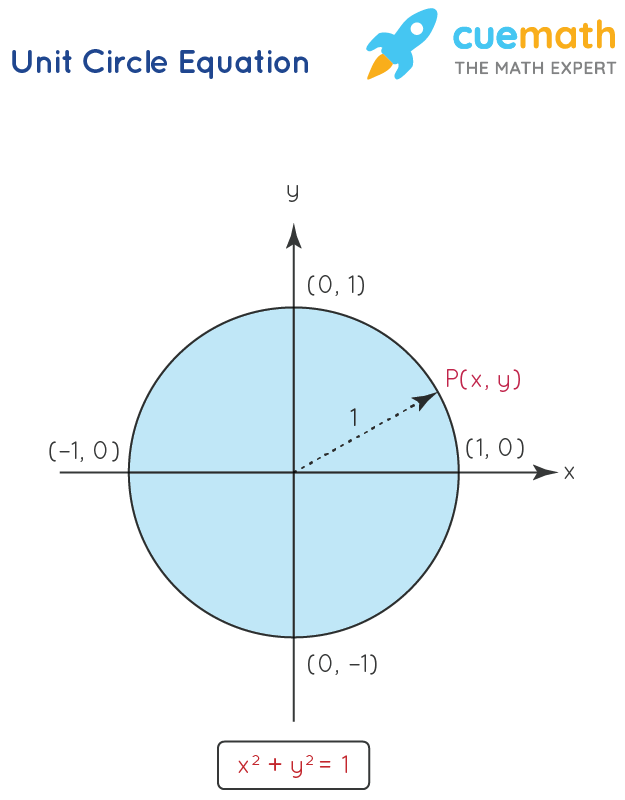
Equation of a Unit Circle \(x^2 y^2 = 1\) Here for the unit circle, the center lies at \((0,0)\) and the radius is \(1\ unit\) The above equation satisfies all the points lying on the circle across theA unit circle is a circle whose radius is 1 unit We can substitute the x and y values into the unit circle equation to determine if the points lie on the unSin ( 90°) Moving 90° 90° counterclockwise around the unit circle from the positive x axis brings us to the top of the circle, where the ( x, y) ( x, y) coordinates are ( 0, 1), ( 0, 1), as shown in

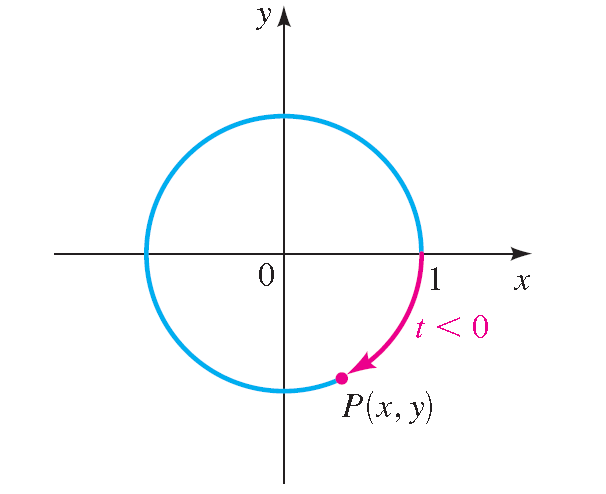
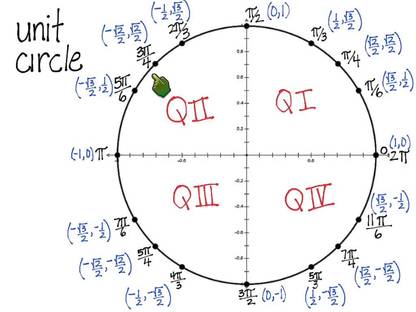
Terminal Points On The Unit Circle

Section 10 2 The Unit Circle Cosine And Sine

The graph of the equation x 2 y 2 = 1 is a circle in the rectangular coordinate system This graph is called the unit circle and has its center at the origin and has a radius of 1 unit TrigonometricAnswer (1 of 4) Use implicit derivative ( basically the chain rule) take the derivative of both sides of x^2 y^2 = 1 ——→ 2x 2y y' = 0 , so y' = x/y at the point (x, y) = which is m ( the slope) atQuestion Show by elimination that x = t^2 − 1/t^21 and y = 2t/ t^21 almost represent the unit circle x^2 y^2 = 1 What point is missing?

Deformation Of The Unit Circle S X 2 Y 2 1 Under The Superflow Download Scientific Diagram

Solved With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used Course Hero

If the {eq}y=b {/eq} is known, then the equation from Step 1 can be written {eq}x^2=1b^2 {/eq} Step 3 Then take the square root of each side of the equation to get two possible solutions forX162 Line Integrals 2 Line integral with respect to x and y In the sum n å i=1 f(x i,y i)Ds i, we can replace Ds i by either Dx i or Dy i, then Definition 2 the line integral of f along C with respect toSTATEMENT 1 Locus of mid point of chords of circle x 2 y 2 = 4 which subtends angle of 2 π at origin is x 2 y 2 = 1 STATEMENT 2 If any chord of circle x 2 y 2 = r 2 subtends an

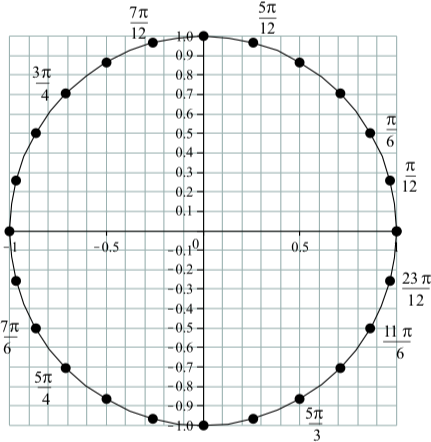
1 1 The Unit Circle Mathematics Libretexts

A Rational Parametrization Of The Circle X 2 Y 2 1 Download Scientific Diagram

You might try x^2 y^2 = 1 y^2 = 1 x^2 y = / sqrt (1 x^2) where / means "plus or minus" Ved Prakash Sharma Former Lecturer atThe unit circle is defined by the equation x^2 y^2 =1 From elementary trigonometry we recall the identity (cos(t))^2 (sin(t))^2 =1 for all 0, 2 p) This directly gives us our first parametrization ofSo P is the point of intersection (in the first quadrant) of the circle x2 y2 = 1 and the line y = x Substituting x for y in the equation of the unit circle x2 x2 = 1 2x2 = 1 x2 = 1/2 k = ± 1/ √ 2

Trigonometric Function The Unit Circle Ppt Download

Unit Circle Trigonometry

 sqrt39/8 or ~~078 In a unit circle, the x coordinate represents the cos value, and the y coordinate represents the sin value Thus, we can say cosx=5/8 From SOHCAHTOA, we know Center = (h,k) = (2,1) And point on circle = (2,3) The equation of circle is given as The distance between center and point on circle is the radius So using the distance formulaAlgebra Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2

Unit Circle Wikipedia

Trig Unit Circle Review Article Khan Academy

In Calculus, most references to the trigonometric functions are based on the unit circle, x2 y2 =1 Points on this circle determine angles measured from the point (0,1)on the xaxis, where theThe unit circle (x 5)^2 y^2 = 1 The ellipse x^2/a^2 y^2/b^2 = 1 The rectangle with vertices at (3, 2), (3, 2), (3, 2), and (3, 2) The unit circle x^2 y^2 = 1 This problem has been solved!Equation of centre of circle (x−h)2 ( y−k)2 = r 2 Substitute h = 0, k

The Set X Consists Of All Points Within And On The Unit Circle X 2 Y 2 1 Whereas Youtube

Trig Identities

How do I write x^2y^2=1 (the unit circle) in terms of y?In mathematics, a unit circle is a circle with a radius of 1 The equation of the unit circle is =The unit circle is centered at the Origin, or coordinates (0,0) It is often used in TrigonometryFinding the function values for the sine and cosine begins with drawing a unit circle, which is centered at the origin and has a radius of 1 unit equals the x value of the endpoint The sine

Complex Numbers Absolute Value

Unit Circle

Answer by ikleyn() (Show Source) YouShow that the point (2, 3) lies inside the circle x 2 y 2 − 6x − 8y 12 = 0 Solution The length of the tangent PT from P(x 1, y 1) to the circle x 2 y 2 2gx 2fy c = 0 is PT = x 1 2 y 1 2A triangle is an isosceles triangle, so the x and y coordinates of the corresponding point on the circle are the same Because the x and y values are the same, the sine and cosine values will

Unit Circle

Unit Circle

Experts are tested byThe unit circle is a name for the circle that has radius 1 and centre (0,0) If a point is on that circle, its coordinates fit the equation x 2 y 2 = 1 If not, it's coordinates don't (5,5) doesn't lie on theIf a variable tangent of the circle x2y2=1 intersects the ellipse x22 y2=4 at points P and Q, then the locus of the point of intersection of tangent at P and Q isA a circle of radius 2 unitsB a

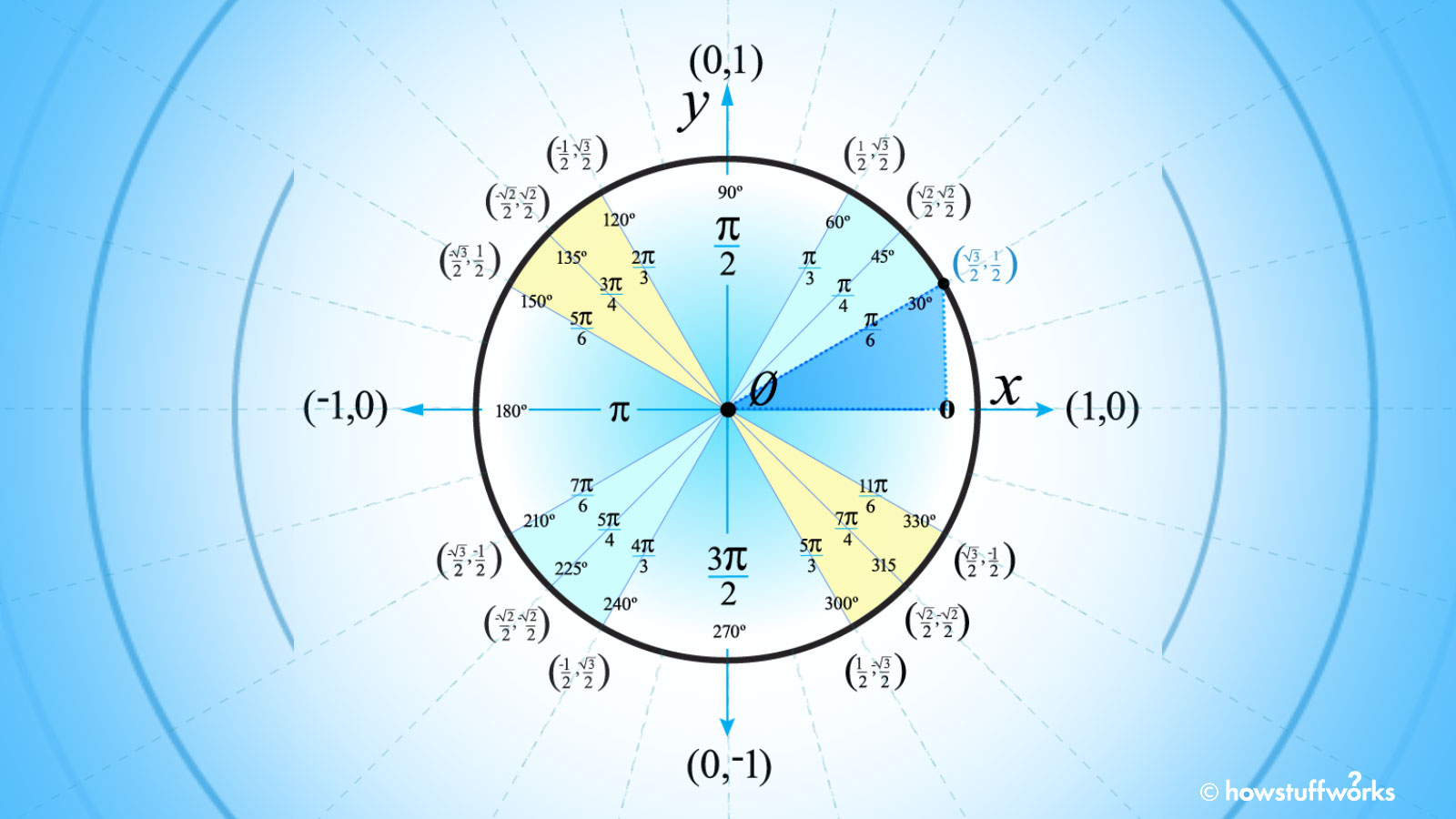
How To Use The Unit Circle In Trig Howstuffworks

Circles

First, we know that x^2=\cos^2 (\theta)=\dfrac {1} {4} x2 = cos2(θ) = 41 we also know y^2=\sin^2 (\theta)=1cos^2 (\theta)=\dfrac {3} {4} y2 = sin2(θ) = 1−cos2(θ) = 43 using another trig identity In the case of a unit circle, the equation is x 2 y 2 = 1 This equation shows that the points lying on the unit circle have to have coordinates (xand yvalues) that, when you square Unit Circle Essential Trigonometric Values Related Pairs for Sine and Cosine Defined by the equation , the unit circle is the collection of points that lie one unit from the origin For

Unit Circle Cost Sint How To Memorize Things Trigonometry Math Formulas

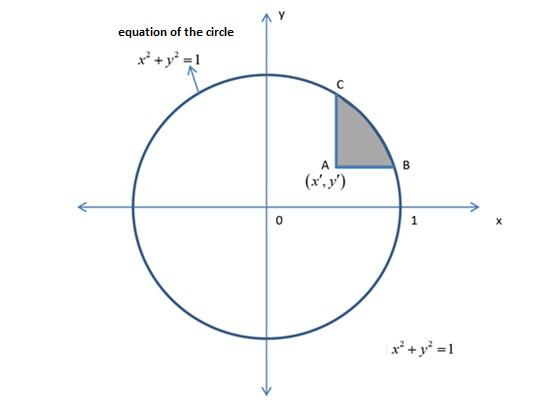
Solved The Unit Circle Is Given For The X And Y Axis In The Chegg Com

 In the case of the right triangle on the unit circle, because the radius (which is also the hypotenuse) is 1, you can say that x 2 y 2 = 1 2 Now replace the x with cos and the y withThe Unit Circle The point of the unit circle is that it makes other parts of the mathematics easier and neater For instance, in the unit circle, for any angle θ, the trig values for sine and cosine areView unit 1docx from MATH 1101 at University of the People Does the equation determine a relation between x and y?

2 1 Plot Of Circle X 2 Y 2 1 And The Definitions Of Cos 8 And Sin Download Scientific Diagram

Determining If A Point Lies Inside Outside Or On A Circle Given The Center Point A Radius Geometry Study Com

 Write the equation of the unit circle concentric with x^2 y^2 – 8x 4y – 8 = 0 asked in Circles by Eeshta01 (304k points) circles; Question 34 Using integration, find the area of the region { (𝑥, 𝑦)" x2 y2 " ≤" 1, x y " ≥" 1, x " ≥" 0, y " ≥" 0" } Here, we are given A circle and a line And we need to find area enclosed

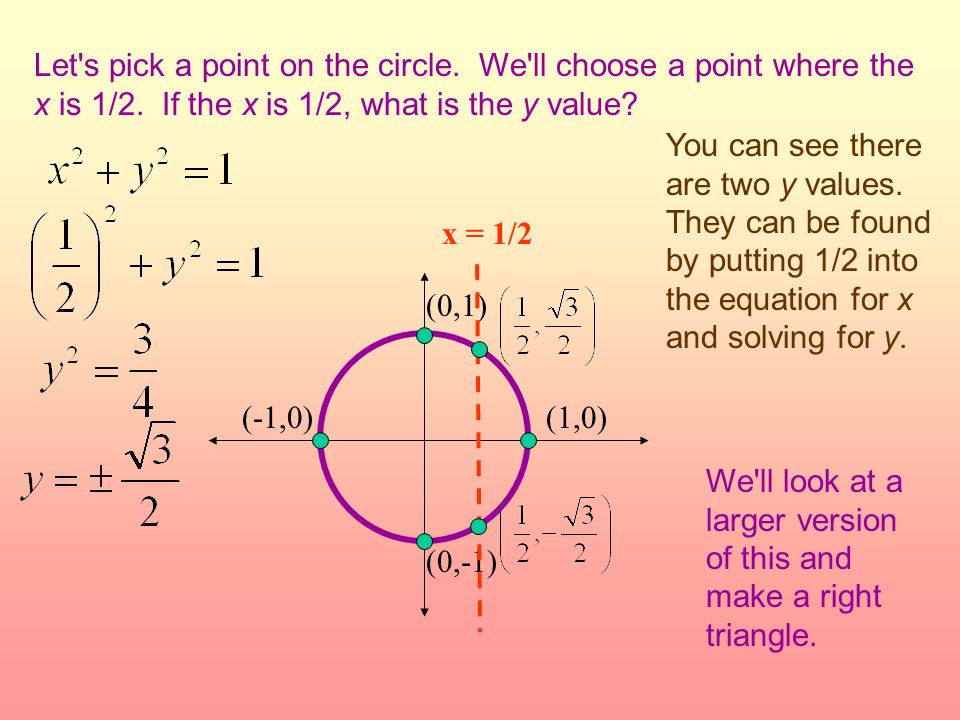
Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download

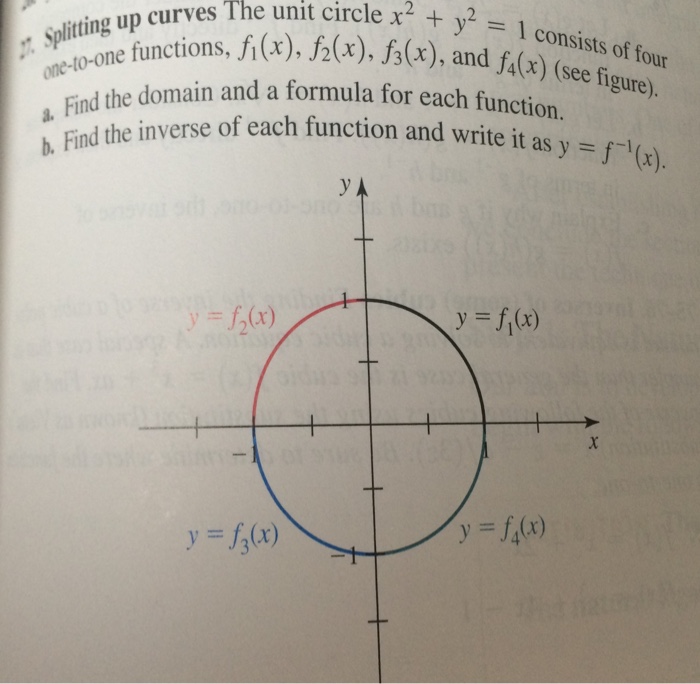
Solved Splitting Up Curves The Unit Circle X 2 Y 2 1 Chegg Com

With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle Study Com

5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts

Solved 1 Consider The Unit Circle X2 Y2 1 A Use Implicit Chegg Com

Unit Circle Wyzant Lessons

Unit Circle

Unit Circle Wikipedia

1

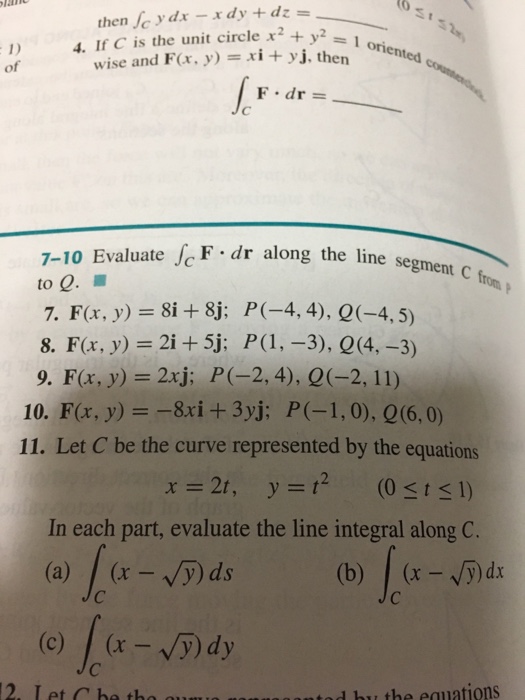
Solved If C Is The Unit Circle X 2 Y 2 1 Oriented Chegg Com

The Set X Consists Of All Points Within And On The Unit Circle X 2 Y 2 1 Whereas The Set Y Consists Of All Points On And Inside The Rectangular Boundary X 0 X

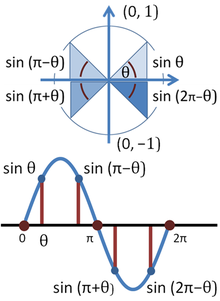
Graphs Of Sine And Cosine Teacher Guide

1 The Unit Circle The Set Of Points At A Distance 1 From The Origin Is A Circle Of Radius 1 The Equation Of This Circle Is X 2 Y 2 1 The Unit Circle Ppt Download

4 2 4 4 The Unit Circle Trig Functions The Unit Circle Is Defined By The Equation X 2 Y 2 1 It Has Its Center At The Origin And Radius 1 0 Ppt Download

Number Theory Variant Of Pythagorean Triples Mathematics Stack Exchange

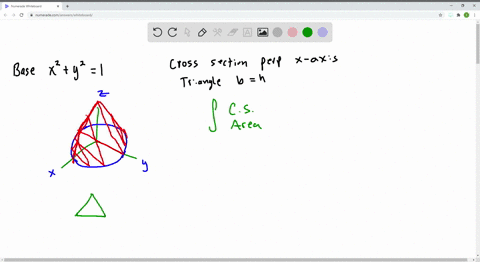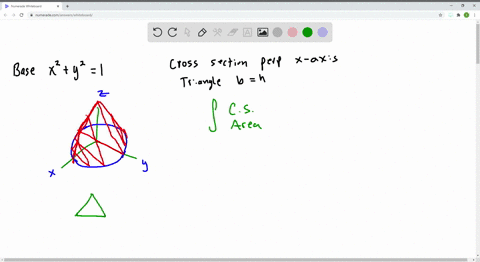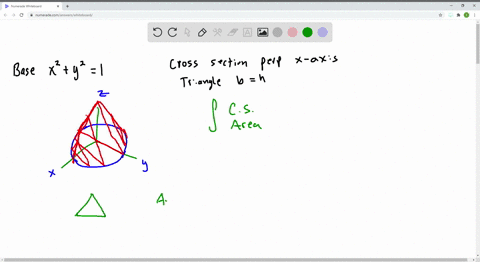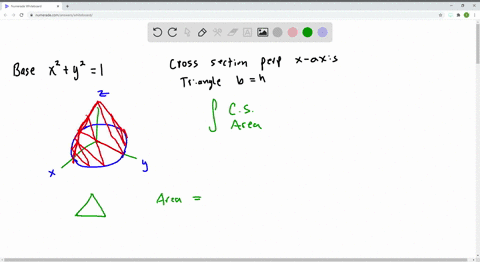
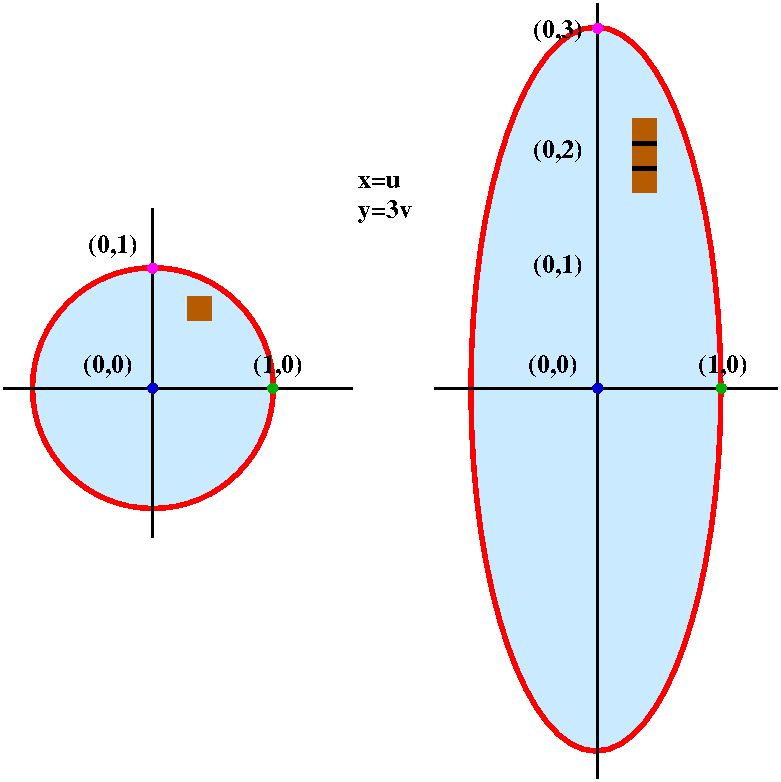
Solved Let B Be The Solid Whose Base Is The Unit Circle X 2 Y 2 1 And Whose Vertical Cross Sections Perpendicular To The X Axis Are Equilateral Triangles Show That The Vertical Cross Sections Have

3 4 Circular Functions X 2 Y 2 1 Is A Circle Centered At The Origin With Radius 1 Call It The Unit Circle 1 0 Ex 1 For The Radian Measure Ppt Download

6 A Plot Of The Unit Circle Satisfying X 2 Y 2 1 Download Scientific Diagram

Unit Circle

Solved On A Unit Circle The Vertical Distance From The X Axis To A Point On The Perimeter Of The Circle Is Twice The Horizontal Distance From The Y Axis To The Same Point What

Paramanand S Math Notes Theories Of Circular Functions Part 1

Solved With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used Course Hero

Real Analysis Unit Circle Is A 1 Manifold In Mathbf R 2 And A Function Is Not A Coordinate Patch Mathematics Stack Exchange

All Of The Points On The Unit Circle Must Satisfy Gauthmath

Unit Circle Trigonometry

Shiny Pebbles And Other Stuff Trig Functions With Almost No Triangles

Unit Circle Equation Of A Unit Circle Unit Circle Chart

4 2 4 4 The Unit Circle Trig Functions The Unit Circle Is Defined By The Equation X 2 Y 2 1 It Has Its Center At The Origin And Radius 1 0 Ppt Download

How To Use The Unit Circle In Trig Howstuffworks

An Object Is Moving In The Clockwise Direction Around The Unit Circle X 2 Y 2 1 Youtube

Unit Circle Wikipedia

How To Use The Unit Circle In Trig Howstuffworks

Unit Circle Trigonometry Learning Math Math Concepts

Math 251 Diary Fall 10

Blank Unit Circle Worksheets Free To Print Now Matter Of Math

Pw Bt3de Fntdm

Unit Circle

Deformation Of The Unit Circle S X 2 Y 2 1 In The Plane Z 1 Download Scientific Diagram

Circles

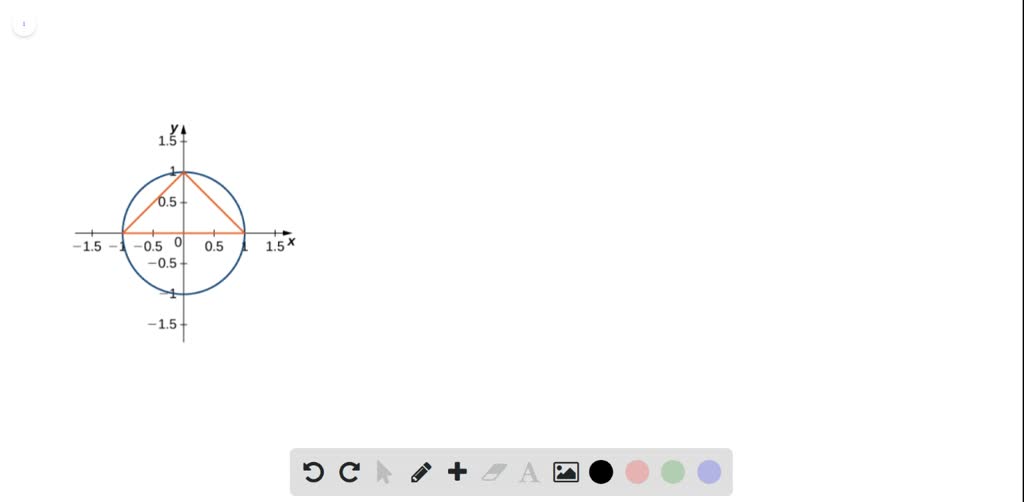
Solved The Largest Triangle With A Base On The X Axis That Fits Inside The Upper Half Of The Unit Circle Y 2 X 2 1 Is Given By Y 1 X And Y 1 X See The Following Figure

1 1 The Unit Circle Mathematics Libretexts

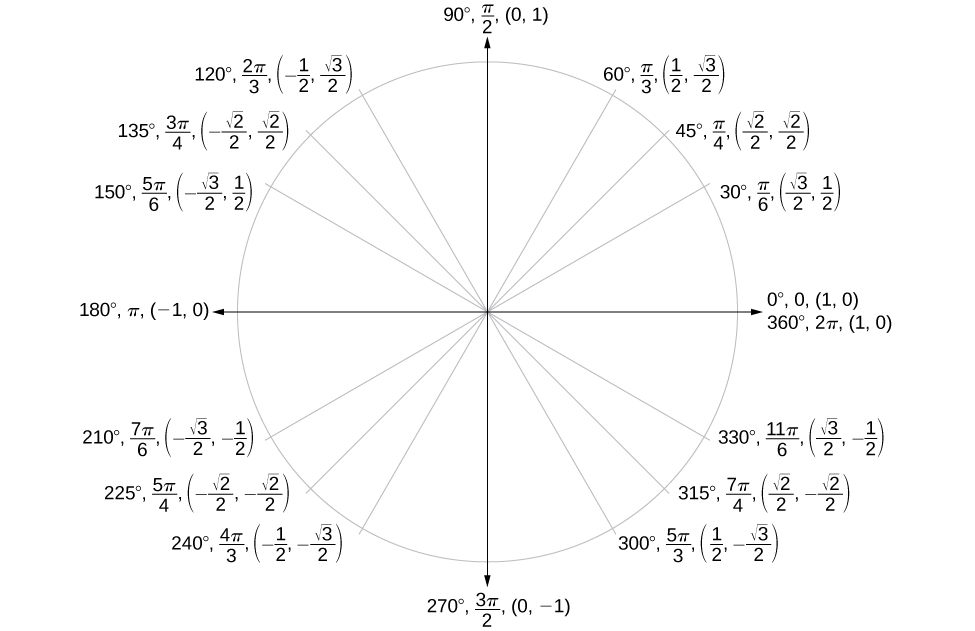
5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts

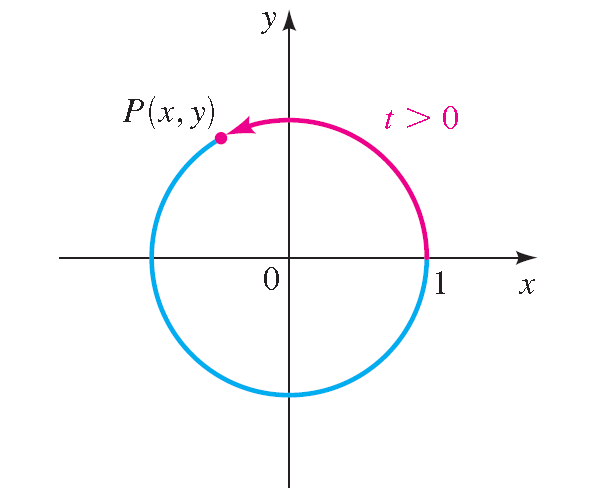
Terminal Points On The Unit Circle

Solved With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used Course Hero

Calculus Prove That The Unit Circle X 2 Y 2 1 Is A Closed Set Mathematics Stack Exchange

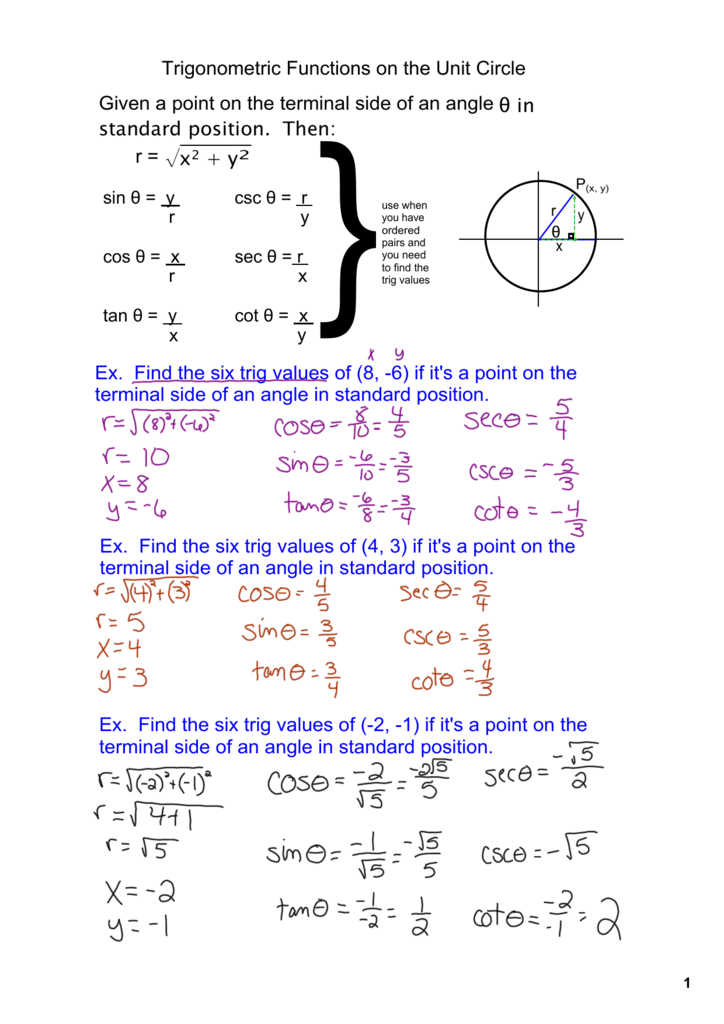
Trigonometric Functions On The Unit Circle Given A Point On The

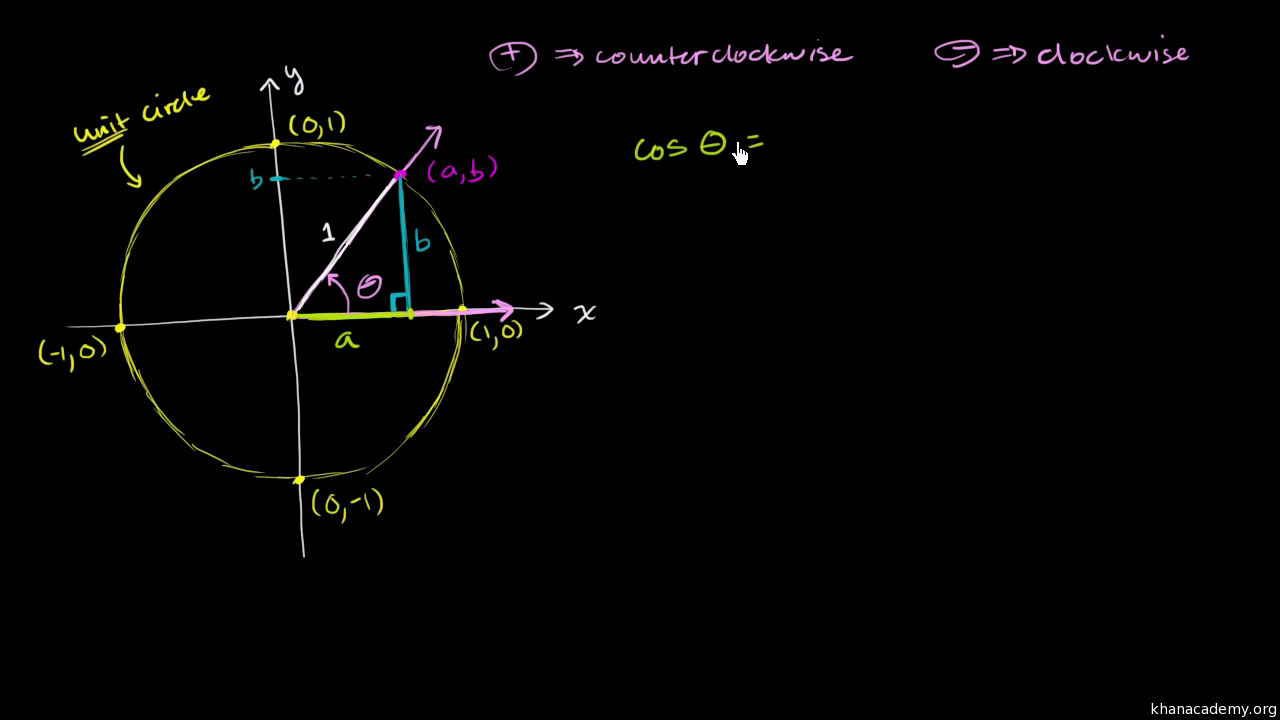
Unit Circle Video Trigonometry Khan Academy

Deformation Of The Unit Circle S X 2 Y 2 1 In The Plane Z 1 Download Scientific Diagram

Do Now Graph The Equation X 2 Y 2 1 Draw And Label The Special Right Triangles What Happens When The Hypotenuse Of Each Triangle Equals 1 Ppt Download

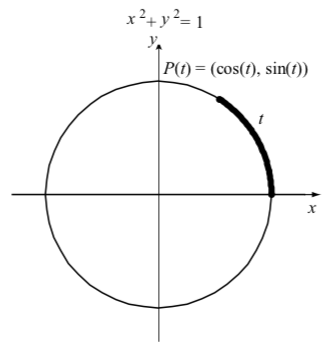
1 2 The Cosine And Sine Functions Mathematics Libretexts

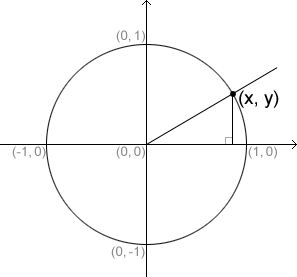
Unit Circle

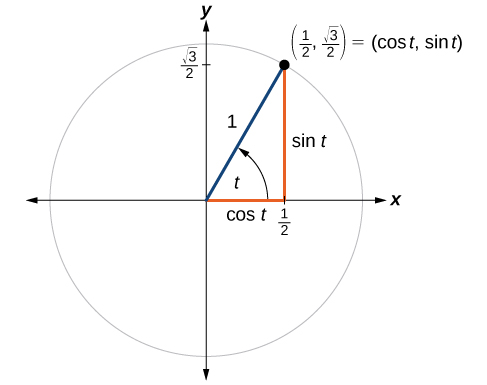
5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts

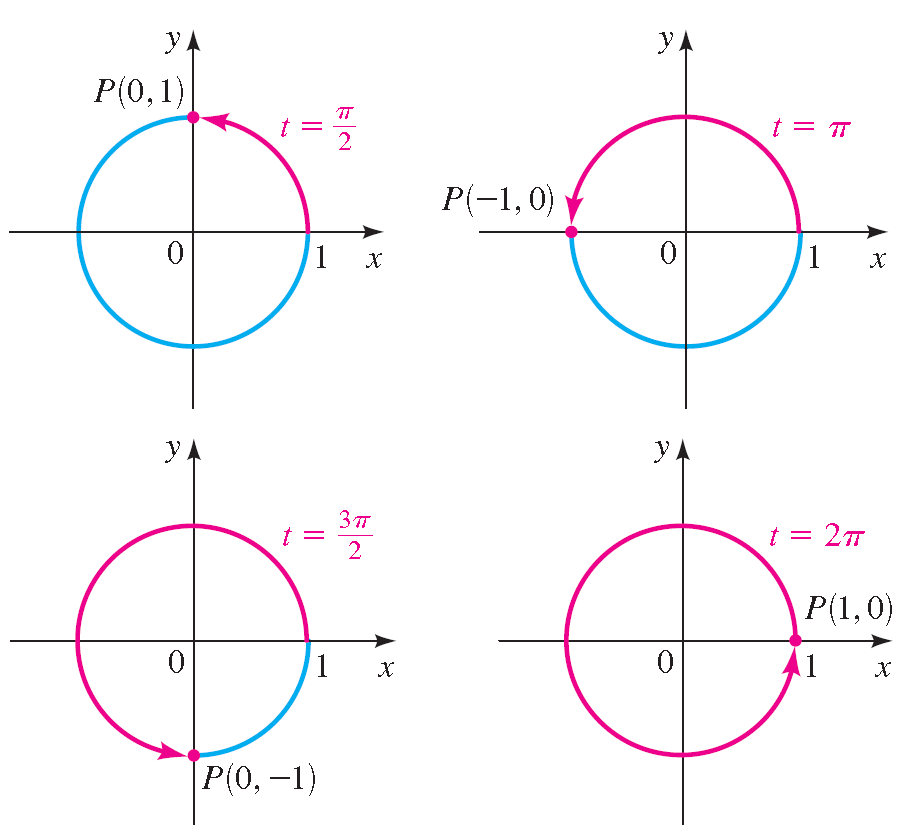
Terminal Points On The Unit Circle

Unit Circle Video Trigonometry Khan Academy

Circles

Solved Consider The Unit Circle C 1 X 2 Y 2 1 And The Chegg Com

Unit Circle Wikipedia

Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download

Unit Circle Calculator Inch Calculator

Measuring Your World

Opencurriculum

3 Let S Denote The Unit Circle X2y2 1 For Each Real Chegg Com

Find A Parameterization For The Circle X 2 2 Y 2 1 Starting At The Point 1 0 And Moving Clockwise Twice Around The Circle Using The Central Angle 0 In The Figure Below

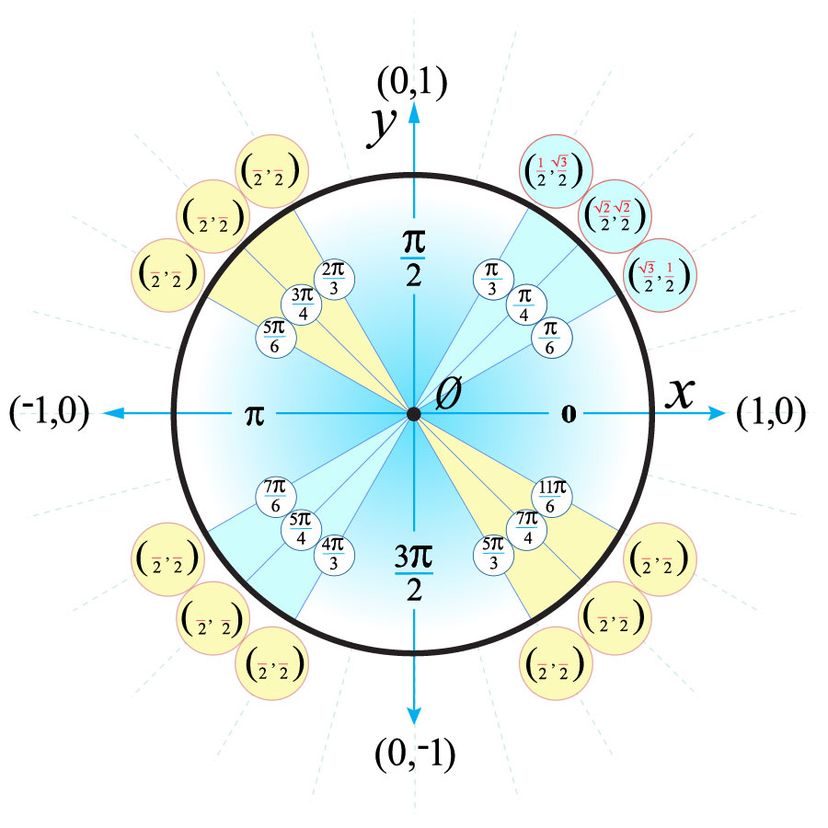
How To Use The Unit Circle In Trig Howstuffworks

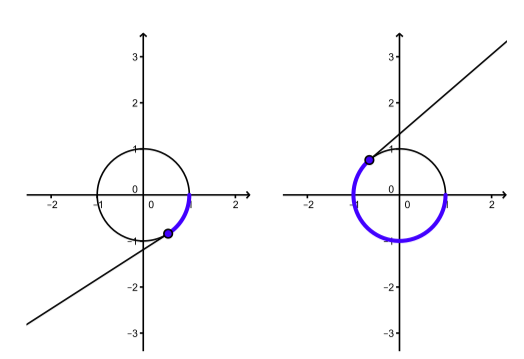
1 1 The Unit Circle Mathematics Libretexts

The Set X Consists Of All Points Within And On The Unit Circle X 2 Y 2 1 Whereas The Set Y Consists Of All Points On And Inside The Rectangular Boundary X 0 X

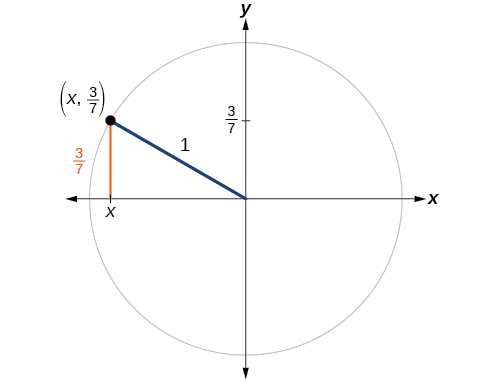
The Point P 1 2 Y Lies On The Unit Circle Show Gauthmath

Solved Consider A Point X Y On The Unit Circle X 2 Y 2 Chegg Com

Incoming Term: unit circle x^2+y^2=1, the base is the unit circle x^2+y^2=1, the equation of the unit circle is x^2+y^2=1, at what points will the line y=x intersect the unit circle x^2+y^2=1,