√ダウンロード 数3 積分 ��題 313595-数3 積分 面積 問��

高校数学 数 動画 不定積分 指数関数編 の問題 19ch

高等学校数学III 積分法/演習問題 出典 フリー教科書『ウィキブックス（Wikibooks）』 3行目から4 行目への変形 数3の不定積分の計算問題です。 θの部分がどうして答えのように表されるのかが分かりません。 お助けください！ 通報する この質問への回答は締め切られました。 質問の本文を隠す A 同じカテゴリの新着質問 A 回答 (1件) ベストアンサー優先

数3 積分 面積 問題

数3 積分 面積 問題- 積分問題1番 2番 3番 4番 5番 6番 7番 8番 9番 10番 11番 12番 13番 14番 15番 16番 17番 18番 19番 番 21番 22番 23番積分, 三角関数 定積分, 和・積の公式 簡単な根号を含む定積分 c 10' 積分 定積分, 置換積分 三角関数の奇数乗の定積分 c 10' 積分, 三角関数 定積分, 置換積分 分母に三角関数と定数の和を含む定積分 c 10' 積分, 三角関数 定積分, 置換積分

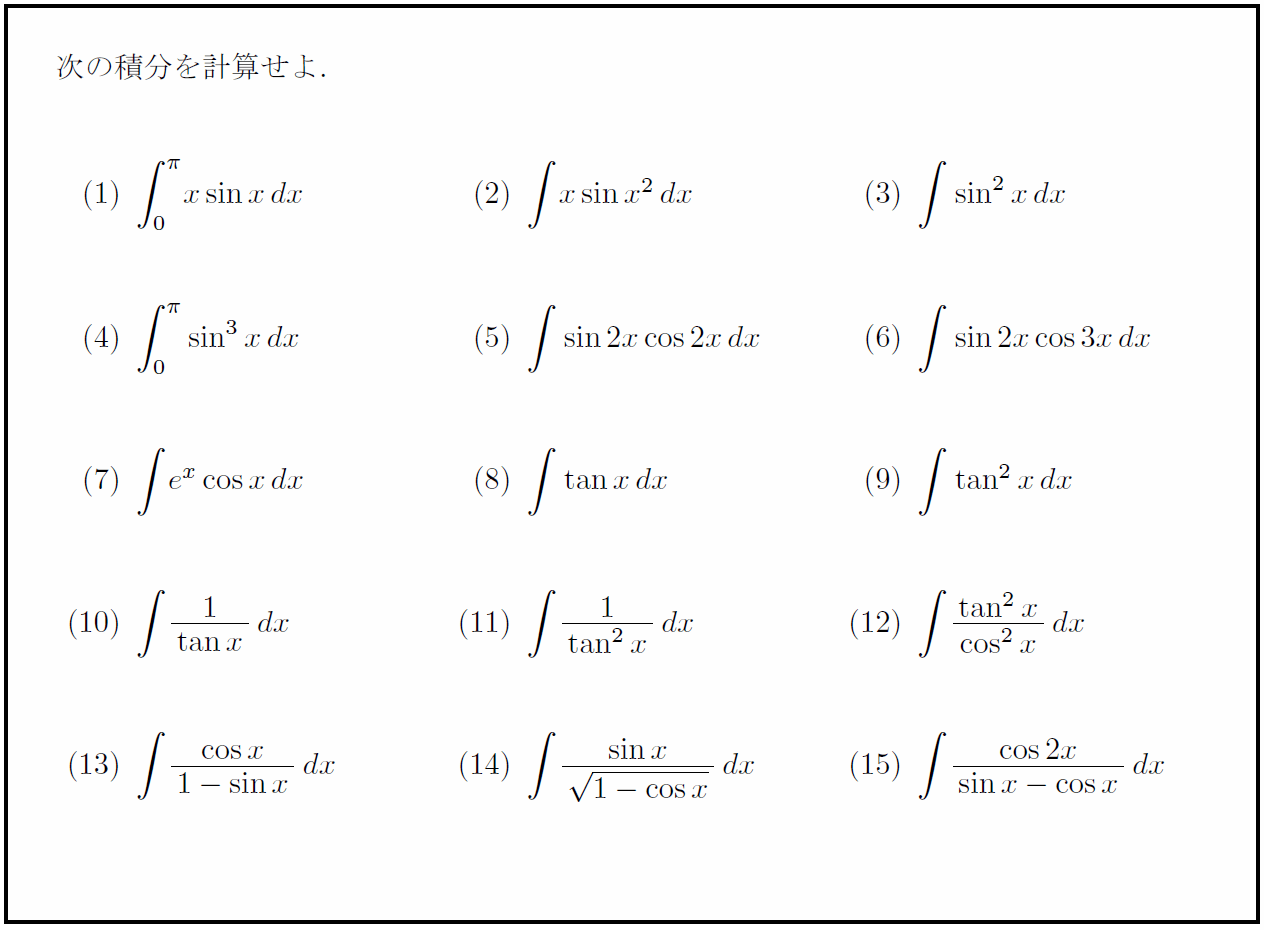
高校数学 三角関数の積分ランダム15題 基本レベル 受験の月

 置換積分法の公式やパターンを見分けるコツをわかりやすく解説 22年1月29日 この記事では、「置換積分法」の公式と、定積分・不定積分における置換積分のやり方をわかりやすく解説していきます。 代表的な置換パターンの見分け方や、ルート・三角積分 複素数 関数 幾何 ベクトル 確率 数列 行列 指数/対数 数と式 その他 問題を解くのに必要な知識を確認するにはこのグラフ図利用してください． 定積分の問題 問題 次の問題を積分せよ。高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** ベクトル解析の公式 展開公式の応用問題（問題の追加） 置き換えによる展開（問題の追加） 展開公式（問題の追加） Google Chart Tools数式 223

PASSLABO特別企画 数3積分150問 解法パターン全解説 （旧帝大入試問題10選＋ランダム積分50選付き） 目次（全パターン解説） 基礎～発展まで Quest1 分数関数（有理関数）の積分 Quest5 三⾓関数のみを含む積分（基本形） Quest61 教科書 問題と解答一覧 教科書（数学Ⅲ）の「積分法」の問題と解答をpdfにまとめました。 「問題」は a3用紙、「解答」は a4用紙で印刷するように作っています。 「問題」は書き込み式になっているので、「解答」を参考にご活用ください。 公開日： 年11月16日 2次試験対策 上野竜生です。 数IIIの「積分」の章末問題として定期試験対策の模擬試験を作りました。 マークシート式で答えるタイプで自動採点もしてくれるので試験対策にぜひ役立ててください。 挑戦してくれた人には模範

数3 積分 面積 問題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張
ある有名な定積分 高校数学 の再掲載 身勝手な主張	ある有名な定積分 高校数学 の再掲載 身勝手な主張

 うさぎでもわかる解析（高校数学・数3） Part07 置換積分：（中身の微分が被積分関数に含まれている場合の）置換積分の省略技 19年7月17日 19年7月17日 14分32秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回も積分についての記事と 問題 解答 \(f(z)=\displaystyle\frac{z(\mathrm{Log} z)^2}{(z1)^3}\) として下の経路で積分。 ① 分子を\((\mathrm{Log} z)^2\)にしていることに注意。

Incoming Term: 数3 積分 問題, 数3 積分 問題集, 数3 積分 面積 問題,